Vektor dan Kinematika

Tak terasa sudah mendekati UTS aja, tapi kali ini bukan UTS seperti zaman SMA dulu yang soalnya pilihan ganda dan ~~nyonteknya gampang banget~~. Untuk membekali UTS, selain dengan belajar latihan soal dari Mathco, Phiwiki, dan Chempro kita juga harus membekali diri dengan konsep-konsep dasar untuk mensiasati soal-soal dengan bentuk baru.

Pada bab pertama kita akan membahas tentang Vektor dan Kinematika Benda Titik, hal serupa pernah dipelajari saat kelas 10 dan 11 SMA namun kali ini akan benar-benar diperdalam.

Vektor

Vektor adalah besaran yang memiliki satuan dan arah, biasa dituliskan dengan:

$\vec{A} = |A|\hat{A}$

dengan:

$\vec{A}$ = Vektor A

$|A|$ = Besarnya (nilai) Vektor A

$\hat{A}$ = Vektor satuan (arah dari) Vektor A

Operasi pada Vektor

Panjang Vektor

Ketika sebuah vektor, misalnya vektor A dituliskan sebagai:

$\vec{A} = a\hat{i} + b\hat{j} + c\hat{k}$

maka panjang dari vektor tersebut sama dengan:

$|A| = \sqrt{a^2 + b^2 + c^2}$

Penjumlahan dan Pengurangan Vektor

Penjumlahan dan pengurangan pada vektor adalah penjumlahan dan pengurangan dari komponen-komponen vektor yang sama. Misalkan vektor A dan B ditulis sebagai:

$\vec{A} = a\hat{i} + b\hat{j} + c\hat{k}$

$\vec{B} = d\hat{i} + e\hat{j} + f\hat{k}$

maka penjumlahan/pengurangan dari vektor-vektor tersebut sama dengan:

$\vec{A} \pm \vec{B} = (a \pm d)\hat{i} + (b \pm e)\hat{j} + (c \pm f)\hat{k}$

Perkalian Skalar (Dot Product)

Perkalian Skalar A terhadap B merupakan panjang proyeksi vektor A di arah B.

Perkalian skalar antara vektor A dan vektor B merupakan panjang proyeksi vektor A pada arah vektor B. Perkalian ini bersifat komutatif dimana 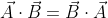$\vec{A}\cdot \vec{B} = \vec{B}\cdot \vec{A}$ . Perkalian skalar memiliki operator cos yang dirumuskan dengan:

$\vec{A}\cdot \vec{B} = |A||B|cos\theta$

Karena itu, jika A dan B ditulis dalam bentuk

$\vec{A} = a\hat{i} + b\hat{j} + c\hat{k}$

$\vec{B} = d\hat{i} + e\hat{j} + f\hat{k}$

jabarkan seperti biasa, seperti perkalian (a+b)(c+d):

$\vec{A}\cdot \vec{B} = ad(\hat{i}\cdot\hat{i}) + ae(\hat{i}\cdot\hat{j}) + af(\hat{i}\cdot\hat{k}) + ... + ce(\hat{k}\cdot\hat{j}) + cf(\hat{k}\cdot\hat{k})$

karena panjang vektor satuan adalah 1 dan operator yang digunakan dalam perkalian skalar adalah cos, maka untuk arah yang sama bernilai 1 (karena cos(0°) = 1) dan untuk arah yang tegak lurus bernilai 0 (karena cos(90°) = 0).

maka, dapat disimpulkan:

$\vec{A}\cdot \vec{B} = ad + be + cf$

Perkalian Vektor (Cross Product)

Arah dari perkalian Vektor A terhadap B mengikuti Right-hand Principle.

Jika perkalian skalar akan menghasilkan produk berupa angka pada akhirnya, berbeda dengan perkalian vektor. Perkalian vektor akan menghasilkan vektor pada hasil akhirnya. Karena itu, perkalian vektor tidaklah komutatif 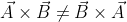$\vec{A}\times \vec{B} \neq \vec{B}\times \vec{A}$ . Namun, terdapat hubungan 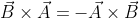$\vec{B}\times \vec{A} = -\vec{A}\times \vec{B}$ . Perkalian vektor memiliki operator sin yang dirumuskan dengan:

$|\vec{A}\times \vec{B}| = |A||B|sin\theta$

Jika kita kembali dengan vektor A dan B yang ditulis dalam bentuk

$\vec{A} = a\hat{i} + b\hat{j} + c\hat{k}$

$\vec{B} = d\hat{i} + e\hat{j} + f\hat{k}$

lalu dijabarkan menjadi

$\vec{A}\times \vec{B}= ad(\hat{i}\times\hat{i}) + ae(\hat{i}\times\hat{j}) + af(\hat{i}\times\hat{k}) + ... + ce(\hat{k}\times\hat{j}) + cf(\hat{k}\times\hat{k})$

perhatikan bahwa operator yang dipakai adalah sin, untuk vektor satuan dengan arah sama akan bernilai 0 (sin(0°) = 0) sementara untuk vektor satuan yang membentuk 90° (i x j, j x k, k x i) akan bernilai 1 (sin(90°) = 1) dan yang membentuk -90° (j x i, k x j, i x k) akan bernilai -1 (sin(-90°) = -1)

maka, dapat disimpulkan:

$\vec{A}\times \vec{B}= bf\hat{i} + cd\hat{j} + ae\hat{k} - ce\hat{i} - af\hat{j} - bd\hat{k}$

hal tersebut sama dengan pola Hukum Sarrus tentang determinan matriks. Karena itu, nilai perkalian vektor juga setara dengan determinan dari matriks:

$\vec{A}\times \vec{B}= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ a & b & c\\ d & e & f \end{vmatrix}$

Kinematika Benda Titik

Posisi

Perpindahan hanya bergantung pada keadaan awal dan akhir, tidak mempedulikan panjang lintasannya.

Posisi adalah letak suatu benda terhadap titik acuan. Kita tidak bisa menentukan posisi mutlak benda apapun tanpa mengetahui terlebih dahulu titik acuannya. Perubahan terhadap posisi, dapat dibagi menjadi 2 bentuk yaitu jarak dan perpindahan.

Jarak: panjang lintasan yang dilewati benda selama selang waktu t.

Perpindahan: perubahan kondisi awal dan akhir benda selama selang waktu t.

Dari hubungan tersebut, maka

$Perpindahan \leq Jarak$

Posisi sendiri sebagai fungsi dapat dinyatakan sebagai:

$\vec{r}(t) = \int \vec{v}(t) dt = \int\int (\vec{a}(t) dt) dt$

Kecepatan

Kecepatan yang dilihat pada speedometer merupakan kecepatan sesaat.

Kecepatan merupakan perubahan posisi terhadap waktu. Ada dua jenis kecepatan, yaitu kecepatan rata-rata selama selang waktu t, yang dirumuskan dengan:

$\overline{\vec{v}} = \frac{r_{2}-r_{1}}{t_{2}-t_{1}}$

Sementara kecepatan sesaat adalah kecepatan saat waktu t, dengan perubahan waktu mendekati 0. sehingga:

$\vec{v}(t) = \lim_{\Delta t \to 0} \frac{\vec{r}(t+\Delta t) - \vec{r}(t)}{\Delta t}$

Karena definisi tersebut adalah definisi turunan, maka:

$\vec{v}(t) = \frac{\mathrm{d} }{\mathrm{d} x}\vec{r}(t)$

Percepatan, Jerk, Jounce, dan Crackle

Pada turunan tingkat tinggi, perubahan-perubahan kecepatan terhadap waktu memiliki namanya sendiri.

Percepatan (Acceleration) : perubahan kecepatan terhadap waktu

$\vec{a}(t) = \frac{\mathrm{d} }{\mathrm{d} x}\vec{v}(t) = \frac{\mathrm{d^2} }{\mathrm{d} x^2}\vec{r}(t)$

Jerk : perubahan percepatan terhadap waktu

$\vec{j}(t) = \frac{\mathrm{d} }{\mathrm{d} x}\vec{a}(t) = \frac{\mathrm{d^2} }{\mathrm{d} x^2}\vec{v}(t) = \frac{\mathrm{d^3} }{\mathrm{d} x^3}\vec{r}(t)$

Jounce : perubahan jerk terhadap waktu

$\vec{s}(t) = \frac{\mathrm{d} }{\mathrm{d} x}\vec{j}(t) = \frac{\mathrm{d^2} }{\mathrm{d} x^2}\vec{a}(t) = \frac{\mathrm{d^3} }{\mathrm{d} x^3}\vec{v}(t) = \frac{\mathrm{d^4} }{\mathrm{d} x^4}\vec{r}(t)$

Crackle : perubahan jounce terhadap waktu

$\vec{c}(t) = \frac{\mathrm{d} }{\mathrm{d} x}\vec{s}(t) = \frac{\mathrm{d^2} }{\mathrm{d} x^2}\vec{j}(t) = \frac{\mathrm{d^3} }{\mathrm{d} x^3}\vec{a}(t) = \frac{\mathrm{d^4} }{\mathrm{d} x^4}\vec{v}(t) = \frac{\mathrm{d^5} }{\mathrm{d} x^5}\vec{r}(t)$

Turunan pada tingkat lebih tinggi lagi jarang sekali digunakan.

GLB dan GLBB

Jika meninjau percepatan benda, terdapat dua kasus yang sering ditemui yaitu Gerak Lurus Beraturan (GLB) terjadi jika a = 0, dan Gerak Lurus Berubah Beraturan (GLBB) terjadi jika a = konstan. Pada nyatanya di dunia nyata, percepatan konstan sangat sulit dilakukan namun dapat dijadikan permodelan yang cukup akurat.

GLB

Pada GLB, a = 0 maka v = konstan. Karena v = konstanta maka:

$\vec{r} = \int \vec{v} dt = \vec{v} \int dt$

Jadi,

$\vec{r} = \vec{v}t + \vec{r}_0$

GLBB

Pada GLBB, a = konstan, maka:

$\vec{v} = \int \vec{a} dt = \vec{a} \int dt$

$\vec{v} = \vec{a}t + \vec{v}_0$

Untuk mencari r, integralkan persamaan v

$\vec{r} = \int \vec{v} dt = \int (\vec{a}t + \vec{v}_0) dt$

$\vec{r} =\frac{1}{2}\vec{a}t^2 + \vec{v}_0t + \vec{r}_0$

Dengan menghilangkan t, persamaan tersebut dapat diturunkan menjadi

$\vec{v_t}^2 = \vec{v_0}^2 + 2a\vec{r}$

Kinematika Dua Dimensi

Gerak Proyektil

Pada gerak proyektil, atau yang disebut dengan gerak parabola, terdapat beberapa cara metode penyelesaian salah satunya adalah dengan memisahkan sumbu x dan sumbu y, yaitu membagi kecepatan awalnya dengan kecepatan awal x dan kecepatan awal y:

$v_0_x = v_0 cos\theta$

$v_0_y = v_0 sin\theta$

Permasalahan di Sumbu X

Pada sumbu x, kecepatan awal tidak dipengaruhi apa-apa sehingga terjadi GLB dengan a = 0.

maka, pada sumbu x berlaku:

$v_0_x = v_x$

$x = v_xt$

Permasalahan di Sumbu Y

Pada sumbu y, kecepatan awal kian menurut dikarenakan percepatan gravitasi yang mengarah ke bawah. Karena itu pada sumbu y terjadi GLBB dengan a = -g. Berlaku:

$v_y = v_0_y - gt$

$y = v_0_yt - \frac{1}{2}gt^2$

Bentuk Lintasan

Apakah benar bentuk lintasan gerak proyektil adalah parabola? untuk membuktikannya maka kita harus membuat grafik dari persamaan gerak proyektil dalam bentuk f(x,y)

$x = v_xt$

$t = \frac{x}{v_{x}}$ ...(1)

substitusikan persamaan 1 ke dalam persamaan sb.y

$y = v_0_yt - \frac{1}{2}gt^2$

$y = v_0_y(\frac{x}{v_x}) - \frac{1}{2}g (\frac{x}{v_x})^2$

Maka persamaan lintasannya adalah:

$y = -\frac{g}{2v_x^2}x^2+\frac{v_0_yx}{v_x}$

karena orde tertinggi adalah 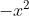$-x^2$ maka dapat dipastikan bentuk lintasannya adalah parabola terbuka ke bawah.

Gerak Melingkar

Gerak melingkar adalah bentuk dari gerak yang memiliki lintasan berupa lingkaran. Lintasan dapat berbentuk lingkaran karena adanya percepatan yang mengarah ke dalam (percepatan sentripetal).

Hubungan antara Gerak Melingkar dan Gerak Lurus adalah sebagai berikut:

$r = \theta . R$

$v = \omega . R$

$a = \alpha . R$

Sementara itu, percepatan sentripetal dirumuskan dengan:

$a_s = \frac{v^2}{R}$

Cari Blog Ini

Adjie Brotot Blog